为什么有些变量不用重复声明
参见threejs源码
three/src/renderers/webgl/WebGLProgram.js
projectionMatrix * modelViewMatrix * vec4(position, 1.0) 是怎么来的
完整公式是 projectionMatrix * viewMatrix * modelMatrix * vec4(position, 1.0)
- projectionMatrix 投影矩阵 (@camera)
- viewMatrix 相机世界矩阵的逆矩阵 (@camera.matrixWorldInverse)
- modelMatrix 模型对象的世界矩阵 (@模型对象)
- position 每个顶点的坐标 (@模型对象)
从右向左进行矩阵相乘: 模型变换(平移/旋转/缩放) => 视图变换 => 投影变换
过程讲解
每个顶点坐标(x,y,z,w)都是相对于物体中心的, 如图

世界中心不变, 只要移动物体的每个顶点就可以将整个物体在世界空间中进行平移缩放或者旋转, 移动时需要计算出平移缩放旋转的矩阵

这样就把物体顶点与世界空间进行了转换, 顶点坐标从物体的相对坐标变成了相对于世界坐标 (model coordinates 通过 modelMatrix 转变成了 world coordinates)

现在需要用相机去观察世界空间, 同样, 相机也是位于世界空间中
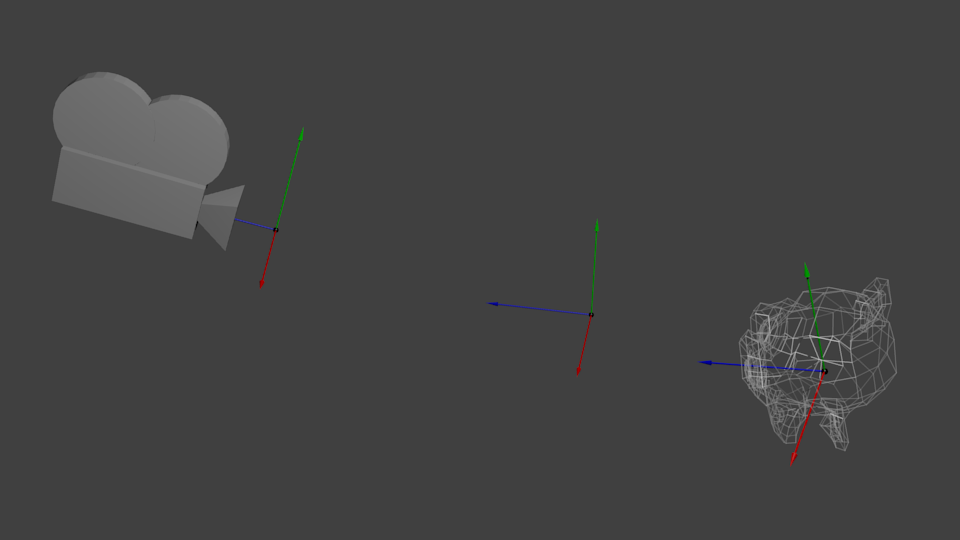
此时移动相机坐标与移动物体同理, 你可以把相机坐标映射到世界空间, 或者反向处理, 将世界坐标映射到相机矩阵中, 两者是等价的, 所以就是 model coordinates 通过 modelMatrix 转变成了 world coordinates, 然后通过 viewMatrix(这里是逆矩阵) 转变成了 camera coordinates

此时相机应用了投影矩阵, 那就把前面得到的 camera coordinates 通过 projectionMatrix 转变成[投影矩阵坐标]

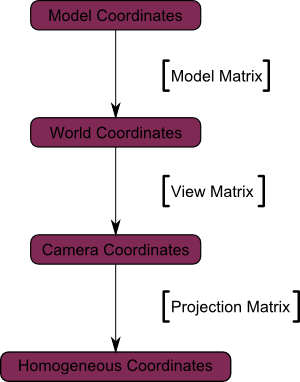
以上就是此公式的计算过程
还有哪些glsl函数
| 函数 | 含义 |
|---|---|
| sin(x) | 正弦函数 |
| cos(x) | 余弦函数 |
| tan(x) | 正切函数 |
| asin(x) | 反正弦函数 |
| acos(x) | 反余弦函数 |
| atan(x) | 反正切函数 |
| pow(x, y) | 幂函数 |
| sqrt(x, y) | 计算平方根 |
| length(x) | 返回向量的长度 |
| distance(x, y) | 返回两个向量的距离 |
| normalize(x) | 标准化向量 |
| min(x, y) | 返回其中较小的值 |
| max(x, y) | 返回其中较大的值 |
| step(edge, x) | 差值(阶梯)函数 |
| smoothstep(edge0, edge1, x) | 差值(平滑梯度)函数 |